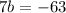Question

Describe the move Dylan made to get each equivalent system. Explain how you know. Write another set of equivalent systems that will allow one variable to be eliminated and enable you to solve the original system.

Answer 1

Given the system of equations:

`\begin{gathered} 12a+5b=-15\rightarrow(1) \\ 8a+b=11\rightarrow(2) \end{gathered}`

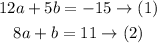
Dylan wrote the following 2 steps

The first step:

`\begin{gathered} 12a+5b=-15 \\ -40a-5b=-55 \end{gathered}`

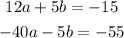
so, he multiplied the equation number (2) by (-5) to eliminate the variable (b)

The second step:

`\begin{gathered} 12a+5b=-15 \\ -28a=-70 \end{gathered}`

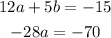
so, he adds equation (1) to the result of step (1)

He eliminated the variable (b), then get an equation with the variable (a) only to solve the equation to find (a)

Now, we will write another set of equivalent systems that will allow one variable to be eliminated and enable you to solve the original system.

So, we will try to eliminate the variable (a)

`\begin{gathered} 12a+5b=-15\rightarrow(*2) \\ 8a+b=11\rightarrow(*-3) \\ ================ \\ 24a+10b=-30 \\ -24a-3b=-33 \end{gathered}`

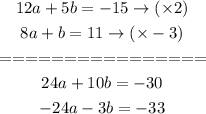
We have multiplied the first equation by (2) and the second equation by (-3)

To get the previous system

The second step is to add the equations to get an equation with the variable (b)

so,

`7b=-63`