From the information provided, the student has achieved three of the required scores and the fourth when added would be used to calculate an average of 60. To calculate the average, the student would use the following approach;
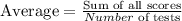
We shall take the unknown test to be x (that is, the fourth test), and then we would have;

ANSWER:
The minimum score on the fourth test would be at least 64.25 to obtain a grade of D