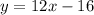Question

Find Slope of Tangent Line:Find the equation of the tangent line to the parabola y = x^3 at the point P(2,8).Use x = 2.1, 2.01, 2.001, 2.0001, 2.00001; 1.9,1.99, 1.999, 1.9999, 1.99999 to find slope

Answer 1

To find the slope of the tangent line, we need to calculate the value of the function in the values of x given, which are very close to the tangency point. Then, using these points, we can find the slope of the tangent line, and after that we find the equation of the tangent line.

So we have that:

`\begin{gathered} y=x^3 \\ x=2.1\to y=9.261 \\ x=2.01\to y=8.12 \\ x=2.001\to y=8.012 \\ x=2.0001\to y=8.0012 \\ x=2.00001\to y=8.00012 \\ x=1.9\to y=6.859 \\ x=1.99\to y=7.88 \\ x=1.999\to y=7.988 \\ x=1.9999\to y=7.9988 \\ x=1.99999\to y=7.99988 \end{gathered}`

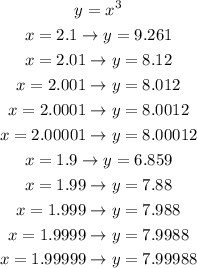
Now, to find the slope of the tangent line, we can use one of the nearest points (x=2.00001 or 1.99999) and the point (2,8) using the formula:

`m=(y_2-y_1)/(x_2-x_1)=(8-7.99988)/(2-1.99999)=(0.00012)/(0.00001)=12`

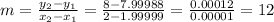
So the slope of the tangent line is 12.

Now, to find its equation, we can use the point (2,8) and the equation y = mx + b with the slope of 12:

`\begin{gathered} y=12x+b \\ x=2\to y=8\colon \\ 8=12\cdot2+b \\ 8=24+b \\ b=8-24=-16 \end{gathered}`

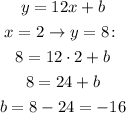
So the equation of the tangent line is:

`y=12x-16`