ANSWER
B. 4 and 6
Step-by-step explanation
The function is partially factored. As we can see, one of the factors is (x - 4), which means that x = 4 is one of the three zeros this function has.
The other two zeros are the zeros of the factor (x² - 12x + 36), so we have to solve,
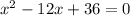
To solve it, we can use the quadratic formula,

In this case, a = 1, b = -12, and c = 36,
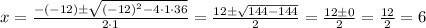
We should have got two zeros, but we only got one since the discriminant is 0. This means that this zero has multiplicity 2.
Hence, the zeros of this function are 4 and 6.