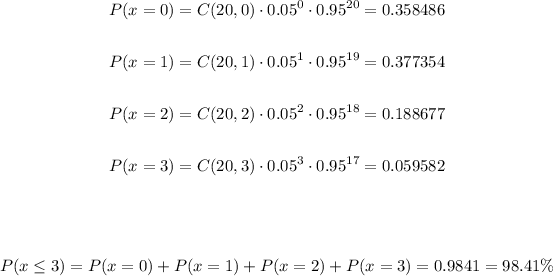Question

I do not understand the factorial! I was told I need to have that in all my work with bionomal probability formula

Answer 1

In order to calculate the probability of k successes among n trials, we can use the formula below:

`P(x=k)=C(n,k)\cdot p^k\cdot(1-p)^(n-k)`

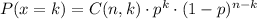
Where C(n, k) is the combination of n choose k:

`C(n,k)=(n!)/(k!(n-k)!)`

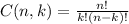
For n = 15, p = 0.4 and k = 4, we have:

`\begin{gathered} P(x=4)=C(15,4)\cdot0.4^4\cdot0.6^(11)\\ \\ P(x=4)=(15!)/(4!11!)\cdot0.4^4\cdot0.6^(11)\\ \\ P(x=4)=(15\cdot14\cdot13\cdot12)/(4\cdot3\cdot2)\cdot0.4^4\cdot0.6^(11)\\ \\ P(x=4)=1365\cdot0.4^4\cdot0.6^(11)\\ \\ P(x=4)=0.12677 \end{gathered}`

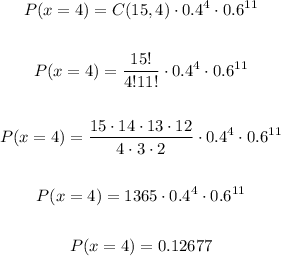
For n = 12, p = 0.2 and k = 2, we have:

`\begin{gathered} P(x=2)=C(12,2)\cdot0.2^2\cdot0.8^(10)\\ \\ P(x=2)=0.28347 \end{gathered}`

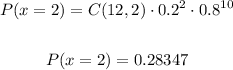
For n = 20, p = 0.05 and k = 0, 1, 2 and 3, we have:

`\begin{gathered} P(x=0)=C(20,0)\cdot0.05^0\cdot0.95^(20)=0.358486\\ \\ P(x=1)=C(20,1)\cdot0.05^1\cdot0.95^(19)=0.377354\\ \\ P(x=2)=C(20,2)\cdot0.05^2\cdot0.95^(18)=0.188677\\ \\ P(x=3)=C(20,3)\cdot0.05^3\cdot0.95^(17)=0.059582\\ \\ \\ \\ P(x\leq3)=P(x=0)+P(x=1)+P(x=2)+P(x=3)=0.9841=98.41\% \end{gathered}`