Let's call L the length of the rectangle and W the width of the rectangle
We know the length is 3 times its width:
L = 3W
The area of a rectangle is:
A=L*W
Substituting the condition above, we have:
A = (3W)*W
Operating:
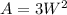
We know the area is 147 yd^2, so we equate:
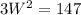
Solve for W:
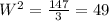
Taking the square root on both sides:
![W=\sqrt[]{49}=7](https://img.qammunity.org/2023/formulas/mathematics/high-school/jglsyrbv0rpg9ti9ixsnnwhh8wyr3seeut.png)
The width is 7 yd. Now we can easily find the length:
L=3W=3*7=21 yd
Finally, we calculate the perimeter of the rectangle. Recall the perimeter is calculated with the formula:
P=2L+2W
Thus, using the known values:
P=2*21+2*7=42 + 14 = 56 yd
The perimeter of the rectangle is 56 yd