Question

Consider the following curve.f(x) = V x2 + 6x – XDetermine the domain of the curve. (Enter your ans(No Response)Find the intercepts. (Enter your answers as comma-y-intercept (No Response)x-intercept (No Response)

Answer 1

Given the function:

`f(x)=\sqrt[]{x^2+6x}-x`

the graph of the function will be as follows:

As shown in the figure:

The domain is the values of x which can be f(x) is valid

As the function contain a square root, so, the root must be greater than or equal to zero

so, the domain will be:

`(-\infty,-6\rbrack\cup\lbrack0,\infty)`

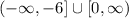
The Y-intercept is the value of y which make x = 0

So, as shown: y-intercept = 0

The x-intercept is the value of x which make y = 0

So, as shown: x-intercept = 0