Question

In an arithmetic series, t10 = 33 and S16 = 432. Find the first three terms.

Answer 1

Step 1 :

In this question, we were given the following:

`\begin{gathered} T_{10\text{ }}\text{ ( 10th term ) = 33} \\ T_{10\text{ }}\text{ = a + ( 10 - 1 ) d = 33} \\ a\text{ + 9 d = 33 --- equ 1} \end{gathered}`
`\begin{gathered} S_{16\text{ }}(sum\text{ of 16 terms ) = 432} \\ S_{16\text{ }}=\text{ }(16)/(2)\text{ ( 2 a + ( 16 - 1 ) d ) = 432} \\ 8\text{ ( }2\text{ a + 15 d ) = 432} \\ \text{Divide both sides by 8 , we have that:} \\ 2\text{ a + 15 d = 54 ---- equ 2} \end{gathered}`

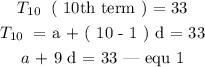
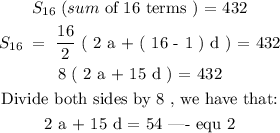
Step 2 :

Next, we need to find the value of a and d from the two sets of equations.

`\begin{gathered} a\text{ + 9d = 33 --- equ 1 x 2 = 2 a + 18 d = 66 -- equ 3} \\ 2\text{ a + 15 d = 54 -- equ 2} \\ \text{equ 3 - equ 2 : } \\ 2a\text{ - 2a + 18 d - 15 d = 66 - 54} \\ 3d\text{ = 12} \\ \text{Divide both sides by 3 , we have that:} \\ d\text{ = 4} \end{gathered}`
`\begin{gathered} \text{put d = 4 in equ 1 , we have that:} \\ a\text{ + 9 d = 33 -- equ 1 } \\ a\text{ + 9 ( 4 ) = 33} \\ a\text{ + 36 = 33} \\ a\text{ = 33 - 36} \\ \text{a = -3} \end{gathered}`

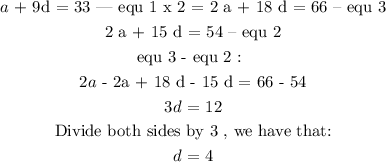
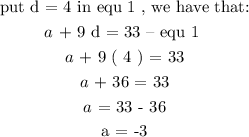
Step 3 :

Next, we need to get the first three terms. To get the terms, we need to evaluate the following:

Recall that a = - 3 and d = 4,

`T_1\text{ = a = -3}`
`T_2\text{ = a + ( 2 - 1 ) d = a + d = - 3 + 4 = 1}`
`T_3\text{ = a + 2 d = - 3 + 2 ( 4 ) = - 3 + 8 = 5}`

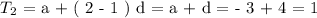
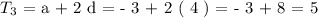
CONCLUSION:

The first three terms are : - 3 , 1 and 5