We know that a linear equation is given generally as:
y = mx + c
where m = gradient
and c = y intercept
We can see from the scatter plot that the y intercept is 1.12
So, already we have limited our options to B and C.
Now let us find our slope with the second and third data points:
(1, 1.15) and (2, 1.18)
Slope is given as:
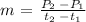
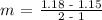
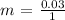
m = 0.03
Which means that if we were to write a linear equation of this, it would be:
P(t) = 0.03t + 1.12
The only option that is close to this is B which is:
P(t) = 0.02t + 1.12
Hence, this is our answer.