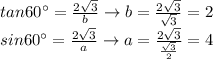Question

Geometry problem: Find the missing side lengths for a and b

Answer 1

`a=4; b=2`

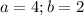
Explanation:

1. The unmarked angle is 30° (since unmarked, +60°, a right angle will add to 180°)

2. Mirror the triangle over the known side. The triangle you get is an equilateral triangle. This allows us to say 2b = a

At this point, pythagorean theorem:

`a^2 = b^2+(2\sqrt3)^2 \rightarrow a^2= b^2+12 \rightarrow\\(2b)^2=b^2+12 \rightarrow 4b^2-b^2 = 12\rightarrow 3b^2=12\\b^2=4 \rightarrow b=2 \implies a=4`

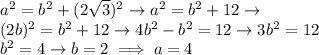
Only the positive solution is taken since it's a length of a segment.

Same result can be obtained with trigonometry if you are allowed to use higher grade math. In particular

`tan 60\° = \frac{2\sqrt3}b \rightarrow b= (2\sqrt3)/(\sqrt3) = 2\\sin 60\° = \frac{2\sqrt3}a\rightarrow a = (2\sqrt3)/((\sqrt3)/(2)) = 4`