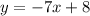The line is perpendicular to the line:
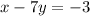
We can rewrite the equation in the slope-intercept form to be:
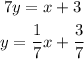
This equation compared to the slope-intercept form will give the slope as follows:
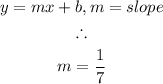
Recall that perpendicular lines have slopes that are negative reciprocals. Thus:
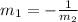
Hence, the slope of the required line will be:
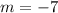
Given that we have the point the line passes through given, we can put the equation in the point-slope form:

At the point (0, 8), we have the equation to be:
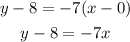
In the slope-intercept form, the equation of the line will be: