Question

Is the set of irrational numbers:closed under addition?YesNoclosed under multiplication?NoYesclosed under subtraction? noyesclosed under division?noyes

Answer 1

Let's test the square root of 2. It is an irrational number and we can use it to know whether or not they are under the given operations.

Addition.

Imagine that you add sqrt(2) to 1-sqrt(2) (that is also an irrational number):

`√(2)+(1-√(2))=1`

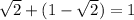
We would obtain 1 as result, and 1 is not an irrational number. It means that irrational numbers are not closed under addition.

Multiplication.

Find the product of sqrt(2) and sqrt(2):

`√(2)\cdot√(2)=2`

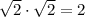
We would obtain 2 as result, and 2 is not an irrational number. Irrational numbers are not closed under multiplication.

Substraction:

Find the difference of sqrt(2) and sqrt(2):

`√(2)-√(2)=0`

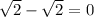
The result is 0, which is a rational number. Irrational numbers are not closed under substraction.

Division:

Find the quotient of sqrt(2) and sqrt(2):

`(√(2))/(√(2))=1`

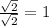
1 is not an irrational number, it means that they are not closed under division.

It means that the set of irrational number is not closed under an