Question

A gas pipeline is to be constructed from a storage tank, which is right on a road, to a house which is 600 feet down the road and 300 feet back from the road. Pipe laid along the road costs $800 per foot, while pipe laid off the road costs $1000 per foot. The gas company would like to run the pipeline for the cheapest amount possible, so they have called on you.***Just to get yourself started, you decide to make the angle in the diagram θ = 28 ∘. Answer each of the following problems based on the given angle. PART ONE:1. What is the length of the pipeline OFF the road? (round to two decimal places)2. What is the cost of the pipeline OFF the road? (use your rounded answer from part 1)3. What is the length of the pipeline ON the road? (round to two decimal places)4. What is the cost of the pipeline ON the road? use your rounded answer from part 3)5. What is the overall cost of the pipeline? (use your rounded answers from part 2 and 4)And solve question 2

Answer 1

We can draw the following picture:

1. What is the length of the pipeline OFF the road?

Since we have a straigh triangle, we can write

`\sin 28=(300)/(h)`

where h is the hypothenuse of the triangle. If we move h to the left hand side, we have

`h\cdot\sin 28=300`

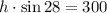
hence, h is equal to

`h=(300)/(\sin 28)`

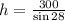
since sin28=0.47, w obtain

`\begin{gathered} h=(300)/(0.47) \\ h=638.29 \end{gathered}`

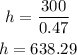
hence, the lenght of the pipeline off the road is 638.29 ft

2. What is the cost of the pipeline OFF the road?

In order to answer this question, we must find x.

We know that

`\cos 28=(600-x)/(h)`

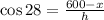
since h=638.29 and cos 28=0.88, we have

`0.88=(600-x)/(638.29)`

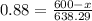
then, we have

`(0.88)(638.29)=600-x`

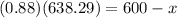
which gives

`563.57=600-x`

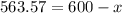
Now, if we move 600 to the left hand side as -600, we obtain

`\begin{gathered} 563.57-600=-x \\ -36.42=-x \\ x=36.42 \end{gathered}`

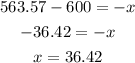
Now, since the pipe laid off the road costs $1000 per foot, we can write

`h\cdot1000`

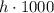
since h=638.29, the cost is

`\begin{gathered} 638.29\cdot1000 \\ 638297.87 \\ \end{gathered}`

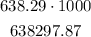
that is, the cost is $638297.87

3. What is the length of the pipeline ON the road? (round to two decimal places)

The lenght is 600-x. This was computed above and its equatl to 563.57 ft.

4. What is the cost of the pipeline ON the road?

This cost is the lenght 563.57 ft times the cost $800, it yields

`563.57\cdot800=450856`

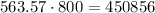
that is, $450,856

5. What is the overall cost of the pipeline?

Its the addition of the two answer above:

`\begin{gathered} 563.57\cdot800+638.29\cdot1000 \\ 450856+638297.87 \\ 1089153.87 \end{gathered}`

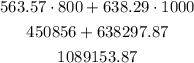
that is, the cost is $1089153.87

Part 2. Now the angle is 61 degrees.

From the triangle, we can compute x and h as:

`\begin{gathered} \sin 61=(300)/(h) \\ \cos 61=(x)/(h) \end{gathered}`

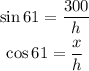
From the first equation, we have

`\begin{gathered} h=(300)/(\sin 61) \\ h=(300)/(0.87) \\ h=344.827 \end{gathered}`

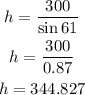
then, x is equal to

`\begin{gathered} x=h\cdot\cos 61 \\ x=344.827\cdot0.484 \\ x=167.175 \end{gathered}`

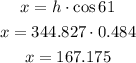
Therefore, the cost is

`\begin{gathered} 800(600-x)+1000h= \\ 800(600-167.175)+1000(344.827) \end{gathered}`

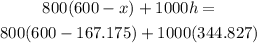
which gives

`\begin{gathered} 346259.6424+344827= \\ 691086.64 \end{gathered}`

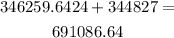
that is, the cost is $691,086.64