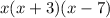SOLUTION
We want to write the polynomial in factored form
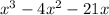
Looking at the last term of the polynomial -21x, we can take a smart guess that one of the zeros or roots of the polynomial would be -3. Now let us put x = -3 into the polynomial, if we get 0, then (x + 3) would be one of its factors, we have
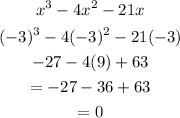
Hence (x + 3) is a factor. Now, dividing the polynomial with (x + 3), we have
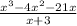
Dividing, we have
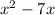
Factoring the polynomial we just got, we have
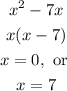
Hence the answer becomes