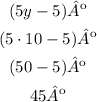Considering the figure:
The horizontal lines are parallel lines crossed by a transversal line, the angles with measure 3xº and 60º are corresponding angles, which means that they are congruent, then:
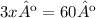
From this expression, you can determine the value of x, simply divide both sides by 3:
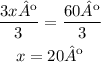
The value of x is 20º
Next, to determine the value of y, you have to work using the quadrilateral on the bottom:
Before you can determine the value of y, you have to determine the measure of the fourth angle of the quadrilateral, which I named "z" for explanation purposes.
The angle with measure 60º and z are supplementary angles, this means that their measures add up to 180º

From this, you can determine the value of z:

You know that the sum of the inner angles of a quadrilateral is equal to 360º, for the quadrilateral marked with red, you can express this as follows:
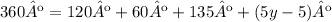
Now we can determine the value of y:
-Simplify all like terms together:

-Subtract 310º to both sides of the equal sign:
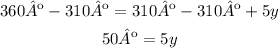
-Divide both sides by 5

The value of y is 10º
You can determine the measure of the angle as follows: