Given that q is an integer that can be expressed as the sum of two integer squares, Let's show that 2q and 5q can also be expressed as the sum of two integer squares.
Let a and b represent the integers.
We have:
a² + b² = q
To show that both 2q can also be expressed as the sum of two integer squares, we have:
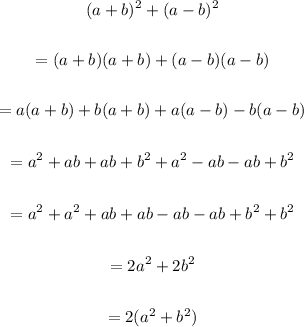
Since a² + b² = q, we have:
2(a² + b²) = 2q
From the above we have shown that 2q can also be expressed as the sum of two integer squares.
• To show that both 5q can also be expressed as the sum of two integer squares, let's apply the expression below:

Using the above expression, we have shown that 5q can also be expressed as the sum of two integer squares.