Question

Using the side lengths, determine what type of triangle would be created, if any.2,4,53,4,56.7.87.9.153, 3, 10** AcuteRight* Obtuse:: Cannot form a triangle

Answer 1

Let a, b,c be the sides of a triangle and c be the larger side.

A triangle can be formed by the sides a,b and c only if,

`\begin{gathered} a+b>c \\ b+c>a \\ c+a>b \end{gathered}`

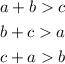
Then, if

`\begin{gathered} c^2=a^2+b^2 \\ \end{gathered}`

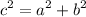
The triangle is right angled.

If,

`c^2>a^2+b^2`

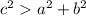
The triangle is obtuse.

If,

Hence, 2,4,5 are the sides of an obtuse angled triangle.

Consider sides 3, 4, 5.

The sum of any two sides is greater than the third side. So, a triangle can be formed by the sides 3, 4, and 5. 5 is the length of the largest side.

`\begin{gathered} 5^2=3^2+4^2 \\ 25=9+16 \end{gathered}`

Hence, 3,4 and 5 are the sides of a right angled triangle.

Consider sides 6,7,8.

The sum of any two sides is greater than the third side. So, a triangle can be formed by the sides 6, 7, and 8. 8 is the length of the largest side.

`\begin{gathered} 8^2<6^2+7^2 \\ 64<36+49 \end{gathered}`

Hence, 6,7 and 8 are the sides of an acute angled triangle.

Consider sides 7,9,15.

The sum of any two sides is greater than the third side. So, a triangle can be formed by the sides 7, 9, and 15. 15 is the length of the largest side.

`15^2>7^2+9^2`

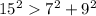
Hence, 7, 9and 15 are the sides of an obtuse angled triangle.

Consider sides 3,3,10.

The sum of any two sides is not greater than the third side. So, a triangle cannot be formed by the sides 3,3 and 10.