we have the function
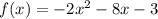
This is a vertical parabola open downward (the leading coefficient is negative)
The vertex is a maximum
The axis of symmetry is the x-coordinate of the vertex
so
Convert the given equation into vertex form
y=a(x-h)^2+k
where
(h,k) is the vertex
x=h ----> axis of symmetry
step 1
Factor -2
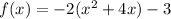
step 2
Complete the square
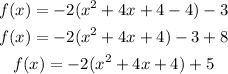
step 3
Rewrite as perfect squares
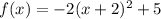
The vertex is the point (-2,5)
The axis of symmetry is x=-2
see the attached figure below