Question

Calculate the total resistance and voltage as well as the current across each resistor inthe parallel circuit found below:

Answer 1

First, we need to find the equivalent resistance. We can find it as follows:

`\begin{gathered} (1)/(Req)=(1)/(R1)+(1)/(R2)+(1)/(R3) \\ so: \\ (1)/(Req)=(1)/(15)+(1)/(5)+(1)/(12) \\ (1)/(Req)=(7)/(20) \\ Req=(20)/(7) \\ Req=2.857\Omega \end{gathered}`

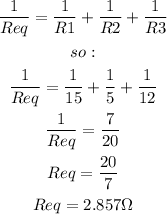
Now, we can find the voltage using Ohm's law:

`\begin{gathered} V=IR \\ so: \\ V=10.5\cdot2.857 \\ V=30V \end{gathered}`

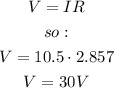
Now, since the circuit is in parallel, the voltage is the same for every resistance. So, let's find the current for each resistance using Ohm's law:

For the resistance of 15:

`I_(15)=(V)/(R)=(30)/(15)=2A`

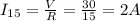
For the resistance of 5:

`I_5=(V)/(R)=(30)/(5)=6A`

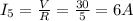
For the resistance of 12:

`I_(12)=(V)/(R)=(30)/(12)=2.5A`

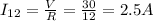
Completing the table using the previous data: