Question

If QT is the perpendicular bisector of PR find each measure geometry perpendicular angle bisectors

Answer 1

Given the shown figure:

As shown, QT is the perpendicular bisector of PR

And SP = SR

SP = 4x + 4 , SR = 7x - 17

So, we can write the following equation:

`7x-17=4x+4`

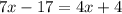
Solve the equation to find (x):

`\begin{gathered} 7x-4x=17+4 \\ 3x=21 \\ x=(21)/(3)=7 \end{gathered}`

QT is the perpendicular bisector of PR

So, the triangle PQR is an isosceles triangle with the vertex Q

So, QP = QR

QP = 5y -31, QR = 2y + 5

So, we can write the following equation: