We have the cost function in function of the number of hamburgers as:C
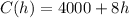
1.1) We have to represent the income I.
It will be equal to the number of hamburgers times the price of each hamburguer ($20).
Then, we can write it as:
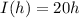
1.2) We have to complete the table for each production level.
We can use the functions to calculate for each level.
We start with the expenses:
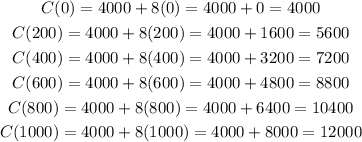
We can now calculate the income I(h) as:
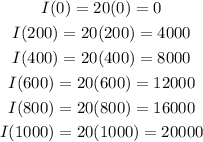
We can then complete the table as:
We now have to graph both functions.
We can use the horizontal axis for h and the vertical axis for C and I and obtain:
1.4) From the graph we know that the amount of hamburguers he need to sell to break even is between 300 and 400, where C(h) = I(h).
We can use the equations to find the exact value:
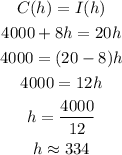
1.5) We can calculate how much he loss when h = 200 as the difference between the income and the cost for that level.
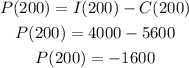
He loss $1600 if he sells only 200 hamburguers.
1.6) We have to calculate h for I(h) = 15000:
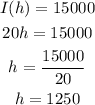
The number of hamburguers is 1250.
1.7) The profit for 1000 hamburguers can be calculated as:
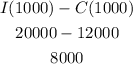
The maximum profit would be $8000.
Answer:
1.1) I(h) = 20h
1.2) Given in the answer
1.4) 334 hamburguers
1.5) He will loss R 1600
1.6) 1250 hamburguers
1.7) R 8000