Question

Solve the right triangle shown in the figure. Round length to one decimal place and express angles to the nearest tenth of a degree.A = 31°, b = 59.4

Answer 1

First, let us solve all the angles.

We are told that the triangle is right; therefore the angle C is 90°. And for angle B, we know that the sum of angles in a triangle is 180°; therefore,

`31^o+B+90^o=180^o`

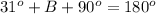
Subtracting 90° from both sides gives

`31^o+B=90^o`

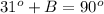
Subtracting 31° from both sides gives

`B=59^o`

Now that we have angles in hand, we now solve for the sides.

Using the cosine ratio we know that

`\cos 31^o=(59.4)/(c)`

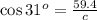
Multiplying both sides by c gives

`c\cdot\cos 31^o=59.4`

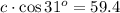
dividing both sides by cos 31 gives

`c=(59.4)/(\cos 31^o)`
`\therefore c=64.9`

Now we find the length a, and for that we use the tangent.

`\tan 31^o=(a)/(59.4)`

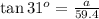
solving for a gives

`a=35.7`

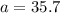
Hence,

A = 31°

B = 59°

C = 90°

a = 35.7

b = 59.4

c = 64.9