Answer:
The first graph is given as
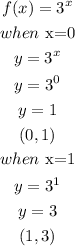
Hence,
The graph is given below as
The second equation is given below as
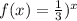
![\begin{gathered} f\mleft(x\mright)=\operatorname{\lparen}(1)/(3))^x \\ when\text{ x=0} \\ f\mleft(x\mright)=\operatorname{\lparen}(1)/(3))^0 \\ f\mleft(x\mright)=1 \\ \lparen0,1) \\ \\ when\text{ x= 1} \\ f\mleft(x\mright)=\operatorname{\lparen}(1)/(3))^1 \\ f\mleft(x\mright)=(1)/(3) \\ \lparen1,(1)/(3)) \\ when\text{ x=-1} \\ f\mleft(x\mright)=\operatorname{\lparen}(1)/(3))^(-1) \\ y=3 \\ \left(-1,3\right) \end{gathered}]()
Hence,
The graph is given below as
The third function is given below as
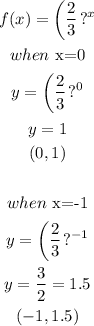
The graph is given below as
The fourth equation is given below
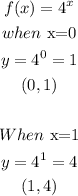
The graph is given below as
Hence,
The final answer is given in the image below as