ANSWER
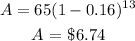
Step-by-step explanation
The initial value of the textbook is given as $65 and it decreases at a rate of 14% per year for 13 years.
Since this is an exponential function, it will be in the form:
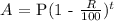
where P = initial value
R = rate
t = time elapsed
A = amount after time t
From the question:
P = $65
R = 16%
t = 13 years
Therefore, the exponential function that models the situation is therefore:
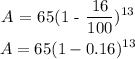
Therefore, the value of the textbook after 13 years is:
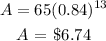
That is the value after 13 years.