Question

Write the coordinates of the vertices after a dilation with a scale factor of 1/5, centered at the origin.B (-5, 5)B' (___,___)

Answer 1

We are asked to determine the coordinates of a point after a dilation centered at the origin. Let's remember that a dilation by a factor of "k" is a transformation of the following form.

`(x^(\prime),y^(\prime))=(kx,ky)`

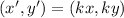
Therefore, in the case where the factor k = 1/5 and the point (x,y) = (-5,5)

`(x^(\prime),y^(\prime))=((1)/(5)(-5),(1)/(5)(5))=(-1,1)`

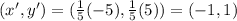
Therefore, the coordinates after the dilation is (x',y')=(-1,1)