Question

how much more interest is earned in 1 year if we compare $50,000.00 at a 3.15% rate, when one account is simple interest and the other compounds weekly?

Answer 1

In the case of the simple annual interest we can calculate what we earn by applying a rule of three. In that case

`\begin{gathered} 50000\rightarrow100 \\ x\rightarrow3.15 \end{gathered}`

Then the anual interest is

`\begin{gathered} x=((3.15)(50000))/(100) \\ =(157500)/(100) \\ =1575 \end{gathered}`

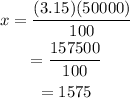
Therefore the simple interest earned in one year is $1575.00.

To calculate the compound interest we have to use the following formula

`A=P(1+(r)/(n))^(nt)`

Where

`\begin{gathered} A\text{ }the\text{ future value including interest} \\ P\text{ }the\text{ initial deposit} \\ r\text{ the annual interest rate in decimal } \\ n\text{ number }of\text{ times that interest is compound } \\ t\text{ }the\text{ time money is invested } \end{gathered}`

In this case we have

`\begin{gathered} P=50000 \\ r=.0315 \\ n=52\text{ (since the year has 52 WEEks)} \\ t=1\text{ (since we want to know what happens after a year)} \end{gathered}`

Then we have

`\begin{gathered} A=50000(1+.(0315)/(52))^((52)(1)) \\ =51599.57 \end{gathered}`

To know the annual interest earned in the second case we have to substract de initial deposit to A, then the annual compound interest we earned is $1599.57.

Finally to know how much interest we earned in the second case we substract $1575.00 to $1599.57.

Then we earned $24.57 more if we compound weekly.