Given:
The mass m1 = 3 kg whose coordinates are (1,2)
The mass m2 = 1 kg whose coordinates are (5,3)
The mass m3= 4 kg whose coordinates are (7,1)
To find the coordinates of the center of mass.
Step-by-step explanation:
The x-coordinate of the center of mass can be calculated as
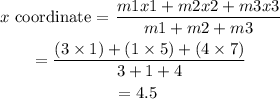
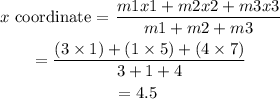
The y-coordinate of the center of mass can be calculated as
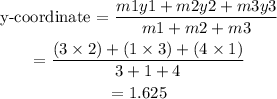
Thus, the coordinates of the center of mass is (4.5,1.625)