Question

Please help 6-13 please I honestly don’t know how to solve this

Answer 1

Given the following trinomial:

`\text{ 2x}^2\text{ + 7x + 4}`

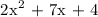
Since the given trinomial is quadratic, there are two factors in this equation.

Step 1: Determine the factors of the first term, 2x².

There are no other possible factors of 2x² but 2x and x.

Therefore, we can now generate the initial factors.

`(2x\text{ + A)(x + B)}`

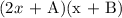
Let A and B represent the unknown constants of the factors to be able to get the product of 2x² + 7x + 4.

Step 2: Let's determine A and B.

Let's think of possible constants of A and B that have a product of 4 and a sum of 7x when adding A multiplied by x and B multiplied by 2x.

Let's list down possible pairs.

TABLE

Sum of 4 (A and B) Sum of 7x

1 and 4 1(x) + 4(2x) = x + 8x = 9x

2 and 2 (2)(x) + 2(2x) = 2x + 4x = 6x

4 and 1 4(x) + 1(2x) = 4x + 2x = 6x

-1 and -4 -1(x) - 4(2x) = -x - 8x = -9x

-4 and -1 -4(x) - 1(2x) = -4x - 2x = -6x

None of the possible factors are possible to complete the equation, therefore, we can say that the given trinomial is not a perfect square and is not factorable.

If we are tasked to factor the trinomial by completing the square, we get:

`\text{ 2x}^2\text{ + 7x + 4}`
`\text{ 2x}^2\text{ + 7x + 4 - 1 = -1}`
`\text{ 2x}^2\text{ + 7x + 3 = -1}`
`\text{ (2x + 1)(x + 3) = -1}`

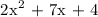
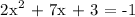
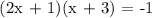
The constant must be 3 and not 4 for it to be factorable and will

give you (2x + 1)(x + 3) = -1.