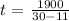Question

A toy company spends $1900 for factory expenses plus $11 per toy truck(t) to make each toy truck.The trucks(t) sell for $30 each. Write the equation in terms of t.(no spaces pr dollar signs)

Answer 1

Given:

Factory expenses = $1900

Cost of each toy truck, t = $11

Selling price of each truck = $30

The equation for this will be:

30t = 1900 + 11t

The equation in terms of t:

First subtract 11t from both sides

30t-11t = 1900+11t-11t

30t-11t = 1900

t(30-11) = 1900

The equation in terms of t is:

`t\text{ = }(1900)/(30-11)`