1 Answer

Ajeet Pratap Maurya · Answer 1 · 2023-05-25T21:12:43+0000

The ball height is 0, when it hits the ground. So

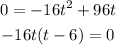
$\begin{gathered} 0=-16t^2+96t \\ -16t(t-6)=0 \end{gathered}$

So from the equation, -16t = 0 or (t - 6) =0.

Evaluate the value of t for the ball hit the ground.

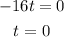
$\begin{gathered} -16t=0 \\ t=0 \end{gathered}$

OR

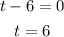
$\begin{gathered} t-6=0 \\ t=6 \end{gathered}$

The ball height is 0 at t = 0 sec and at t = 6 sec.

The t = 0 sec represent the initial condition and t = 6 sec represents the time after which ball hit the ground again.

So answer is t = 6 seconds.

PART B.

Differentiate the equation and equate to 0 for maximum height.

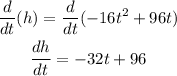
$\begin{gathered} (d)/(dt)(h)=(d)/(dt)(-16t^2+96t) \\ (dh)/(dt)=-32t+96 \end{gathered}$

For maximum height,

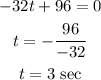
$\begin{gathered} -32t+96=0 \\ t=-(96)/(-32) \\ t=3\text{ sec} \end{gathered}$

So part B answer is 3 sec

Answer:

Part A: 6 seconds

Part B: 3 seconds

Please log in or register to add a comment.