Question

Please help me !! Find the missing length indicated.

Answer 1

Explanation:

use the law of Cosines so that you can solve a SSS triangle

Cos(C) =
`a^(2)` +
`b^(2)` -
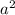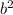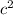`c^(2)` / 2ab

c is the side of 24 for our triangle and angle C is the top one in the picture.

C = arcCos (
`a^(2)` +
`b^(2)` -
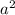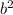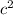`c^(2)` / 2ab )

C = arcCos ( -32 / 480 )

C = 93.82255373 °

the angles at the top are each half of that or 46.91127 °

let's solve another angle for the big triangle now let's go for the one on the left and call it A

Cos(A) =
`c^(2)` +
`b^(2)` -
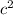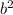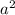`a^(2)` / 2bc where a = 20

A = arcCos(
`c^(2)` +
`b^(2)` -
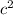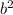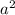`a^(2)` / 2bc)

A = arcCos(
`24^(2)` +
`12^(2)` -
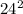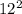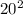`20^(2)` / 2*12*24

A = arcCos(320 / 576)

A = 56.2510 °

then angle B is 180 =93.823 + 56.251 + B

29.926 ° = B

so now we know all 3 angles.. seems like a lot of work , huh :D

for the triangle with the question mark we now know two angles and the Hyp, so let's use Law of Sines to find that last side :)

Sin(A)/a = Sin(B) /b where A can be the angle at the top and B can be the angle at the base. which we have to find still :/

it's 180 = 46.9112 + 29.926 + B

103.162 = B

Sin(46.91127 ) / a = Sin(103.162) /20

Sin(46.91127 ) * 20 / Sin(103.162) = a

14.99998 = a I feel confident this is supposed to be 15 and I have a tiny bit of rounding error..

? = 15 there you go

your answer is 15