ANSWER
C. V = 7x²π + 56xπ + 112π
Step-by-step explanation
The volume of a cylinder is the product of the cylinder's height and its base area. The base is a circle, so the base area is π times the radius squared,
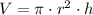
In this problem, the radius is r = (x + 4) and the height is 7 units,
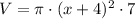
Expand the square using the perfect trinomial squared formula,
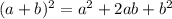
In this case, a = x and b = 4,
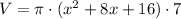
And multiply each term by 7π,
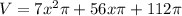
Hence, the expression that represents the volume is V = 7x²π + 56xπ + 112π.