Question

use the guidelines of this section to sketch the curvey =
`\frac{ {x}^(3) }{ {x}^(3) + 1}`

Answer 1

`y=\frac{x^3}{x^3+\text{ 1}}`

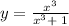
Is this function correct?

This function does not exist when x = -1 becuase

(-1)^3 + 1 = -1 + 1 = 0

and the denominator can not be zero.

This is the graph, as you can see, it does not exist when x = -1

Denominator, how to find the point in which the function does not exist.

`\begin{gathered} \text{ x}^3\text{ + 1 = 0} \\ \text{ x}^3\text{ = -1} \\ \text{ x}^{\text{ }}=\text{ }\sqrt[3]{-1} \\ x\text{ = -1} \end{gathered}`

We need to equal the denominator to zero

and then solve for x

the result is the number in which the function does not exist.