Question

What is the electric resistance of a copper wire 0.65 m long with a diameter of 2 mm?​​

Answer 1

3.5 × 10⁻³ Ω

Explanation:

The resistance of a conductor is calculated by the formula:

• 
  `\displaystyle R=\rho \cdot (l)/(A)`
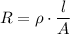
• where R = electric resistance (Ω), ρ = resistivity (Ω · m), l = length of the wire (m), A = area of the cross-section of the wire (m²)

Let's start by converting the diameter of the copper wire to meters.

• 2 mm → .002 m

Since we want the radius of the cross-section, we will divide .002 m by 2.

• .002/2 = .001 m

The radius of the copper wire is .001 m. We can calculate the area of the circular cross-section by using the formula:

• 
  `A=\pi r^2`
• 
  `A= \pi (.001)^2`
• 
  `A= \pi \cdot 10^-^6`

The area of the cross-section is π · 10⁻⁶ m².

The length of the wire is 0.65 m long. We do not have to convert units for the length of the wire since it is already in the SI units: meters.

Assuming the copper wire is at 20°C, we know that its resistivity is 1.7 · 10⁻⁸ Ω · m.

Using these three variables, we can solve for R in the formula for electric resistance.

• ρ = 1.7 · 10⁻⁸ Ω · m
• l = 0.65 m
• A = π · 10⁻⁶ m²

Substitute these values into the equation.

• 
  `\displaystyle R=\rho \cdot (l)/(A)`
• 
  `\displaystyle R=(1.7 \cdot 10^-^8\ \Omega \cdot \text{m}) \cdot \frac{0.65 \ \text{m}}{(\pi \cdot 10^-^6 \ \text{m}^2 )}`
• 
  `\displaystyle R=\frac{(1.105 \cdot 10^-^8 \ \Omega \cdot \text{m}^2)}{(\pi \cdot 10^-^6 \ \text{m}^2)}`
• 
  `R=.3517324242 \cdot 10^-^2 \ \Omega`
• 
  `R=.003517324242 \ \Omega`

Notice how the unit m² cancels out, leaving us with Ω (units of electrical resistance).

The electric resistance of a copper wire 0.65 m long with a radius of .001 m is .0035 ohms (Ω), or 3.5 × 10⁻³ Ω.

Answer 2

To calculate resistance, we will use the formula:

R = ρl / A

where ρ(rho) is the resistivity of the material, l is the length of the wire and A is the cross-sectional area

We are given:

Length of wire (l) = 0.65 m

Diameter of wire (d) = 2 mm

Material of wire: Copper

Some important conversions:

- radius of the wire = diameter/2

radius = 2 mm/2 = 1 mm OR 1 * 10⁻³m

Calculating the cross-sectional area:

Cross-sectional area is the area of the circle at the end of the wire.

Cross-sectional area = π(r²)

Area = π(1 * 10⁻³)² [replacing the value of r]

Area = π * 10⁻⁶ m²

Calculating the resistance:

using the formula mentioned before:

R = ρl / A

R =
`(1.7 * 10^(-8)ohm*m ) * (0.65 m)/(3.14 * 10^(-6)m^(2))` [resistivity of copper = 1.7 × 10⁻⁸ Ωm]

R = 3.52 * 10⁻³ (approx)