Question

Construction the augmented matrix that corresponds to the following system of equations

Answer 1

We want to construct the augmented matrix for these equations;

`\begin{gathered} 4x+(4y-z)/(3)=2 \\ 2(3z-7x)+y-3=1 \\ x-(7+z)=6y \end{gathered}`

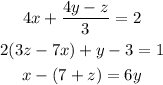
We start by writing the equations with variables on the right and constants on the left; multiplying equation 1 by 3, we have;

`12x+4y-z=6`

Expanding equation 2 and collecting like terms, we have;

`\begin{gathered} 6z-14x+y-3=1 \\ -14x+y+6z=4 \end{gathered}`

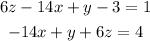
Expanding equation 3 and collecting like terms, we have;

`\begin{gathered} x-7-z=6y \\ x-6y-z=7 \end{gathered}`

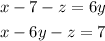
Writing the 3 equations, we have;

`\begin{gathered} 12x+4y-z=6\text{ }i \\ -14x+y+6z=4\text{ }ii \\ x-6y-z=7\text{ }iii \end{gathered}`

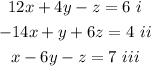
Putting this in augmented matrix form we have;

`\begin{bmatrix}{12} & {4} & {-1} & {6} \\ {-14} & {1} & {6} & {4} \\ {1} & {-6} & {-1} & {7} \\ {} & {} & {} & {}\end{bmatrix}`

Which is the final answer