Question

The minimum wage in 1970 was 1.60. In 2000 it was 5.15. Assume the wage is increasing exponentially. Estimate the minimum wage for 2013. Based on this model, when will the minimum wage be 10.00

Answer 1

• The estimated minimum wage for 2013 is 8.55.

,

• In 2017, the minimum wage will be around 10.00.

Explanation:

The general form of an exponential model is given as:

`f(t)=ab^t`

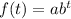
In 1970, The minimum wage was 1.60. i.e.

• When time, t = 0, f(t) = 1.60

`\begin{gathered} 1.60=a(b)^0 \\ \implies a=1.60 \end{gathered}`

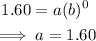
Substitute a=1.60 into f(t).

`f(t)=1.60(b)^t`

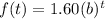
Next, in 2000 it was 5.15.

• When t=2000-1970=30, f(t)=5.15.

Substitute these values into the formula above:

`5.15=1.60(b^(30))`

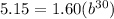
We solve the equation for b.

`\begin{gathered} \text{ Divide both sides by 1.60} \\ (5.15)/(1.60)=b^(30) \\ 3.21875=b^(30) \\ \text{ Take the 30th root.} \\ b=3.21875^{(1)/(30)} \end{gathered}`

Thus, our exponential model f(t) is:

`f(t)=1.60(3.21875^{(t)/(30)})`

(a)Minimum Wage in 2013

In 2013, t=2013-1970=43

`\begin{gathered} f(43)=1.60(3.21875^{(43)/(30)}) \\ f(43)=8.55 \end{gathered}`

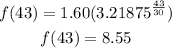
The estimated minimum wage for 2013 is 8.55.

(b)When the minimum wage, f(t)=10.00

We want to find the time, t.

`\begin{gathered} f(t)=1.60(3.21875^{(t)/(30)}) \\ 10=1.60(3.21875^{(t)/(30)}) \end{gathered}`

The equation is solved for t below:

Thus, approximately 47 years after 1970, which is in 2017, the minimum wage will be 10.00.