As the test scores are suppose to distribute normally, we can calculate probabilities with the formula:
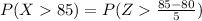
Where Z is a normal distribution, with mean 0 and standard deviation 1
Therefore calculating the number on the right if the Z variable, we find
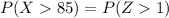
Therefore, we have to calculate the probability that the standard normal distribution is greater than 1
For this, we use a normal table, like the next picture
This table is used in the following manner
You have to ook in the column in the left the number that yoy want to the probability be less than
In our case, we want the probability to be greater than 1
So, we have to do a little trick to get the correct expression
To get a probability for a normal distribution to be greater than a number, we apoly the formula
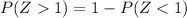
Or in a graph this can be represented as :
Now, returning to our problem we have\;
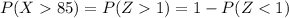
The last probability on the right we will calculate using the table posted above
Searching the number 1 into the column on the left in the table, we find that the probability of this event is :
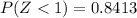
Therefore, we can conclude that:
