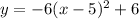Question

Identify the vertex, roots, and equation of the function below.

Answer 1

The equation of a parabola in vertex form, is:

`y=a(x-h)^2+k`

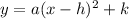
Where (h,k) are the coordinates of the vertex.

From the given graph, notice that the coordinates of the vertex are:

`(5,6)`

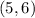
The roots are the values of x where the graph crosses the x-axis. In this case, the graph crosses the x-axis at the points (4,0) and (6,0). Then, the roots are:

`\begin{gathered} x_1=4 \\ x_2=6_{}_{} \end{gathered}`

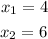
Substitute the values of the vertex into the equation of the parabola in vertex form:

`y=a(x-5)^2+6`

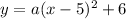
To find the value of a, substitute (x,y)=(4,0):

`\begin{gathered} 0=a(4-5)^2+6 \\ \Rightarrow0=a(-1)^2+6 \\ \Rightarrow0=a+6 \\ \Rightarrow-6=a \\ \Rightarrow a=-6 \end{gathered}`

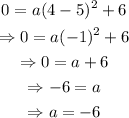
Therefore, the equation of the parabola is:

`y=-6(x-5)^2+6`