Question

Simplify this radical expression → √45x²y³

Answer 1

Given the following expression:

`\sqrt[]{45}(x^(2)y^(3)​)`

You can simplify it following the procedure shown below:

1. You need to descompose the Radicand (the number 45 inside the radical symbol into its Prime Factors:

`45=3\cdot3\cdot5`

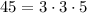
Remember that the Product of powers property states that:

`(b^m)(b^n)=b^((m+n))`

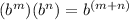
Then:

`45=3\cdot3\cdot5=3^2\cdot5`

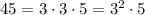
2. Rewrite the expression:

`=\sqrt[]{(3^2\cdot5)}(x^2y^3​)`

3. Remember the following property for Radicals:

`\sqrt[n]{a^n}=a`

Then, simplifying, you get that the answer is:

`\begin{gathered} =3\sqrt[]{(5)}x^2y^3​ \\ \end{gathered}`