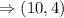Answer:
The question can be explained using the image below
The given coordinates are
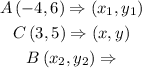
The center is the midpoint of Diameter AB, therefore, we will use the formula for the midpoint of a line given below as
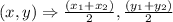
By substituting the values, we will have
![\begin{gathered} (x,y)\operatorname{\Rightarrow}((x_(1)+x_(2)))/(2), ((y_(1)+y_(2)))/(2) \\ \left(3,5\right)\Rightarrow(\left(-4+x_2\right))/(2),(\left(6+y_2\right))/(2) \end{gathered}]()
By equating both equations, we will have
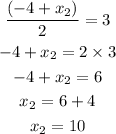
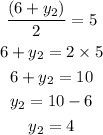
Hence,
The coordinate of B is