According to the statement, to find the distance between Omar's home and the mountains we need to use a system of equations.
Taking x as the average rate and a y as the distance, we know that the distance equals the average rate times the hours that the trip took.
In this case, in the way to the mountains the distance y is x times 6 which was the number of hours that the trip took.
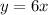
In the way home, the distance y is x plus 22 (because the average rate was 22 faster) times 4 which was the number of hours that the trip took.
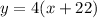
Make both expressions equal and find the value of x:
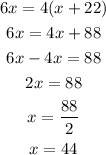
The average rate was 44 in the trip to the mountains, use this value to find the distance:
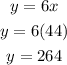
Omar lives 264 miles far way from the mountains.