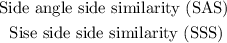:
To check if the triangles are similar, let us take ratios of corresponding sides on both triangles, if they are the same, they are similar, else they are not.
We have:
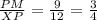
We also have for triangle ALW
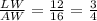
We see that the sides share the same ratios, so the two triangles are similar under the similarity relation