To find the 70th percentile we look for the z value that gives the following probability:
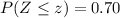
Looking at the standard normal distribution table we notice that this probability happens when:
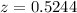
Then we need the z score to be 0.5244 .Now that we know this we use its definition to find the value of x that gives this z score:
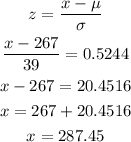
Therefore, the 70th percentile is 287.45