Given
The equation 2 cos²x + 3 = -cos x + 4.
To solve for all values of x on the interval [0, 2π].
Step-by-step explanation:
It is given that,
The equation 2 cos²x + 3 = -cos x + 4.
That implies,
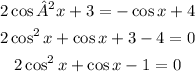
Substitute cosx = a.
Then,
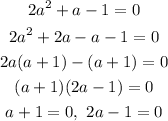
That implies,
![\begin{gathered} \cos x+1=0,\text{ }2\cos x-1=0 \\ \cos x=-1,\text{ }2\cos x=1 \\ \cos(x)=-1,\text{ }\cos(x)=(1)/(2) \\ x=\cos^(-1)(-1),\text{ }x=\cos^(-1)((1)/(2)) \\ x=\pi,\text{ }x=(\pi)/(3),\text{ }2\pi-(\pi)/(3)[since\text{ }cosine\text{ }is\text{ }positive\text{ }in\text{ }the\text{ }1^(st)\text{ \& }3^(rd)\text{ }quadrant] \\ x=\pi,\text{ }x=(\pi)/(3),\text{ }(5\pi)/(3) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/sp6eecadzgl779k09nyyprjwc6g0t2xj00.png)
Hence, the solution is, x=π, π/3, 5π/3.