Question

TRIGONOMETRY Find c in degrees round to the nearest tenth

Answer 1

In this problem, we were given a triangle with the measurements for two of its sides and one angle. We need to use the available information, to determine the value of the angle C in degrees.

For that, we will use the law of sines, which is shown below:

`(\sin A)/(a)=(\sin B)/(b)=(\sin C)/(c)`

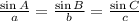
Where A, B, C are the angles for the triangle, and a, b, c are the opposite side from those angles.

We need to find the value of angle C, and we have angle A, therefore we will use:

`(\sin A)/(a)=(\sin C)/(c)`

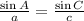
Replacing the data from the problem on the expression above, we obtain:

`\begin{gathered} (\sin(70))/(15)=(\sin C)/(14) \\ \sin C=(14)/(15)\cdot\sin (70) \\ \arcsin (\sin C)=\arcsin ((14)/(15)\cdot\sin (70)) \\ C=61.29º \end{gathered}`

The value of angle C is approximately 61.3°