Question

Safe wheelchair ramp specifications require about 4.75° maximum angle to be constructed with the ground. At a particular building, the owner is installing a wheelchair ramp that needs to rise 3 feet off the ground. The owner insists on constructing the angle with the ground at 2º. How much horizontal distance will the ramp cover with these specifications?

Answer 1

To solve the exercise, it is convenient to first draw a picture of the situation that the statement describes:

Now, you can use the trigonometric ratio tan(θ):

`\tan (\theta)=\frac{\text{ Opposite side}}{\text{ Adjacent side}}`

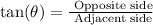
So, you have

`\begin{gathered} \tan (\theta)=\frac{\text{ Opposite side}}{\text{ Adjacent side}} \\ \tan (2\text{\degree})=\frac{3\text{ ft}}{x} \\ \text{ Multiply by x from both sides of the exercise} \\ \tan (2\text{\degree})\cdot x=\frac{3\text{ ft}}{x}\cdot x \\ \tan (2\text{\degree})\cdot x=3\text{ ft} \\ \text{ Divide by tan(2\degree) from both sides of the exercise} \\ \frac{\tan(2\text{\degree})\cdot x}{\tan(2\text{\degree})}=\frac{3\text{ ft}}{\tan(2\text{\degree})} \\ x=\frac{3\text{ ft}}{\tan(2\text{\degree})} \\ x=85.91\text{ ft} \end{gathered}`

Therefore, a horizontal distance of 85.91 feet will cover the ramp with these specifications.