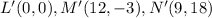When we dilate a figure centered at the origin by a factor k, the new coordinates will be equal to the old coordinates multiplied by the scale factor.
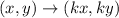
The original vertices of our figure are:
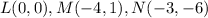
Then, dilating our figure with a scale factor equal to -3, we have:
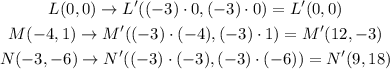
The coordinates of the image are