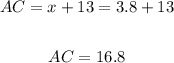Question

Pls help.. im stuck on the setup of the problem .

Answer 1

Given the right angle triangle ABC

As shown, there is a line segment perpendicular to the base AC that produces another two right-angle triangles

From the similarity of the triangle:

`\begin{gathered} (x)/(7)=(7)/(13) \\ \\ x=(7\cdot7)/(13)=3.76923 \end{gathered}`

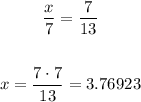
Rounding to the nearest tenths

So, the answer will be:

`x=3.8`

Now, we will find the length of AC

as shown:

`\begin{gathered} AC=x+13=3.8+13 \\ \\ AC=16.8 \end{gathered}`