Let the number of kilograms of type B in 1 bag of blend be b
Given:
(a) There are 4kg of type A in 1 bag
Total kg in 6 bags is 48
Hence:
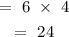
There would be 24kg of type A in 6 bags
Similarly for type B:
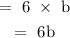
There would be 6b kg of type B in 6 bags
The sum of the of kg of type A and type B in 6 bags is equal to 48
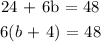
Answer: 6(b + 4) = 48
(b) The number of kilograms of type B in 1 bag
Solving the equation above, we have:
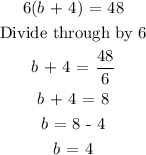
Hence, there are 4kg of type B in 1 bag
Answer: b = 4