Question

What is the quotient of the synthetic division problem below, written in polynomial form? -11 7 15 9

Answer 1

Given the Synthetic Division shown in the exercise, you can find the Quotient as follows:

1. Write down the first coefficient below the horizontal line:

2. Multiply the coefficient by -1 (the number on the left):

`(1)(-1)=-1`

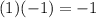
3. Write the result obtained below the second coefficient (in this case this is 7) and add them (write the sum below the horizontal line).

Then:

4. Multiply the number -1 on the left of the box by the Sum obtained:

`(-1)(6)=-6`

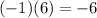
5. Write the Product below the third coefficient and add them.

6. Write the sum below the horizontal line.

Then:

7. Multiply the number -1 by the Sum 9:

`(-1)(9)=-9`

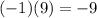
8. Write the Product below the last coefficient and add them.

9. Write the sum below the horizontal line.

Then:

As you can notice, you obtained these coefficients of the Quotient:

`1,6,9`

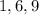
These are the coefficients of the new polynomial. Therefore, you get that this has this form:

`x^2+6x+9`

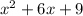
Hence, the answer is: Option A.